TEM images allow further insights into the atomic structure of vitreous carbon networks
February 11, 2014 - In a new study, published in the journal "Scientific reports" from the Nature publishing group, researchers explore further the atomic structure of glass.
Concepts of glass were greatly inspired by the intuition of Zachariasen about random networks for more than 80 years [1, 2]. With the participation of SALVE scientists it was experimentally confirmed in previous studies [3, 4], that the real structure of vitreous regions in silica comes actually very close to the illustrations of Zachariasen (see also the SALVE news article about 2D silica). However, whether these are intrinsic parts of the glass or constitute a separate phase could not be answered experimentally due to limited sample size and consequently limited statistics. Therefore the investigation of these questions remains in the realm of theoretical models and computer simulations [5, 6]. The presence of crystalline regions in glass gave credibility to the crystallite theory [1], which posits that a glass is a disordered arrangement of small crystalline particles separated by a disordered network. In 2010 a ratio of up to 50% crystallites has already been found in amorphous sputtered silicon [7], which supported but not finally answered this open question. An answer to this question could be obtained by an observation of the formation of glass at the atomic level. But the traditional production of glass by cooling a liquid [e. g. 8] makes this impossible.
Now 4 researchers, among which are former SALVE member Jannik Meyer and SALVE director Ute Kaiser have now found a way to observe the transition from crystalline to amorphous phase on the atomic level. They produce disorder in graphene using an electron beam in the electron microscope, but the material remains in the solid phase. The 2-dimensionality of graphene allows it to observe all the atoms directly, thus bypassing the imaging problem of conventional materials. The added disorder manifests itself in the formation of non-hexagonal carbon rings due to the removal of atoms [9] or bond rearrangements [10]. The process can be observed at any stage because, as previously shown [11], graphene remains flat even after formation of 5- and 7-corner polygons.
The stages of the transformation from crystalline to amorphous phase
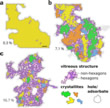
In the initial stage of the experiment small isolated defects are created (Fig. 1a). Under continuous irradiation these grow until they form a vitreous network separating the original crystal into nanometer-sized crystallites (Fig. 1b). During the experiment holes occur in the graphene layers. These form, however, due to chemical effects caused by the electron beam [9] and are therefore not considered as part of the disordered structure. In the final stage the crystallites vanish into the growing network (Fig. 1c). "The determination of the exact atomic configuration from the TEM images was done manually in the past, which is both, cumbersome and faulty. Therefore, the image analysis has until now been limited to relatively small isolated defects. We have for the first time analyzed larger image areas with the assistance of computers", says Jannik Meyer.
Analysis of the atomic structures
Figure 2 shows some examples of atomic structures, which were determined from TEM micrographs, where three regimes are highlighted: (a) Crystalline areas with isolated defects, (b) crystalline regions and glass and (c) random network. Figure 2a shows the first regime with some isolated defects. After increasing the irradiation dose, the defects grow and start to connect. It is noteworthy that isolated crystalline regions remain, which are connected by a glass-like network. An example of such a case, where isolated crystallites can be clearly identified, is shown in Fig. 2b. The resulting structures have some similarity with polycrystalline graphene with micrometer-sized grains [12, 13], however, the glass-like network is much larger than typical graphene grain boundaries [14 - 16] and covers a much larger part of the area. After further irradiation, the glass-like surfaces grow at the expense of the crystalline regions and the structure virtually has no more extended hexagonal faces and can be well described by the random network theory. The final state is shown in Fig. 2c, where the glassy areas clearly dominate the structure.
Amount of order at the shortest scale
In contrast to glass-like oxides such as silica, which consists of polyatomic tetrahedral structural units, the basic building block in this new study is the carbon atom. Therefore the shortest possible order of magnitude for disorder in this material is the connection between adjacent structural units [1]. In order to quantify this disorder, the scientists calculated the distribution function of the interatomic distances. Example cases for different stages of transformation are shown in Fig. 3a-c. Although the deviation from ideal interatomic distances (Fig. 3a) already occurs in the initial stage of the crystalline to the glass transition (Fig. 3b, s. Fig. 3e for the structure), the disappearance of the long-range order is not complete without having reached the crystallite structure (Fig. 3c, see Fig. 3f and 2b for the structure). At this stage the radial distribution function of the interatomic distances is very similar to that found for 2D silica glass [3].
In order to gain a better understanding of the matter under investigation during the transformation, the researchers calculated the ring-statistics, i. e. the distribution of atoms per ring. Fig. 4a-d show the results for 4 different stages: (a) the very first recorded TEM pictures, (b) the first stage with disordered phases (for example, the structure in Figure 3e), (c) the stage of the crystallites shown in Figure 2b and 3f, and (d) the completely disordered phase at the end of the experiment. The increase of non-hexagonal carbon rings with advancing stage can be seen in the distribution functions. Surprisingly, however, hexagons dominate the statistics even in the stage of the highest degree of disorder (Fig. 4d). This observation was not possible in the study of 2D silica [3] due to insufficient amount of data. With the now presented study of graphene, the scientists were able to account for a complete structure for the first time. A comparison of these two studies with reference to the lognormal probability distribution (Fig. 4e) shows that the ratio of non-hexagonal polygon remains almost constant but is different for graphene and vitreous silica. E. g. the ratio of pentagons to heptagons is 1.14 +/- 0.02 throughout the experiment for carbon-glass, but between 1.3 and 1.6 for the vitreous silica 2D [3]. The knowledge of this parameter enables the controlled prediction of structural changes in graphene under the electron beam [17] and glass-like structures in general.
From their database the researchers could now for the first time calculate the evolution of the ratio of hexagons to all other polygons in the structure (crystallinity C) for the transition between pristine graphene and vitreous structures. For pristine graphene C = 1 for vitreous silica structures C < 0.4 [e. g. 3] The result plotted in Fig. 4f supports the hypothesis that the discontinuity marks the actual transition point between crystalline graphene and the glassy phase.
Amount of order at longer scale
In order to analyze the degree of disorder at longer scale, the scientists analyzed the density variations in the final structure (Fig. 2c) on different length scales. For this they divided the structure in square-shaped regions with different widths (w = 0.2 .... 2.0 nm) and calculated the distribution of calculated densities as a function of w (Fig. 4g, h). As expected the density variation decreases when the width increases, i. e. the structure appears more homogeneous on a longer scale. Anyway, as can be seen in the data Figure 4h the fit follows 1/w behavior, which is exactly what one would expect from a completely random network (or "white noise"). This indicates the absence of long-range density fluctuations. [18]
This study shows that the two competing theories of the structure of glass, the nano-crystalline theory and the random network model, provide complementary descriptions on the same material, each applying to a specific range of disorder, at least in two dimensions. "Aberration-corrected electron microscopy is virtually unparalleled in terms of the picture of defective 2D materials with atomic resolution. In modern aberration-corrected TEM instruments and for very thin samples, one can also interpreted the obtained images directly as the projected atomic structure," says Ute Kaiser. "The new investigation of '2D carbon glass' is a further key component to the continued improvement of our understanding of vitreous structures."
Highlighted Topics
Resource: Eder, F. R., Kotakoski, J., Kaiser, U., & Meyer, J. C. (2014). A journey from order to disorder—Atom by atom transformation from graphene to a 2D carbon glass. Scientific reports, 4, doi: 10.1038/srep04060, [PDF], see also the Supplementary Information
Wright, A. C. (1994) Neutron scattering from vitreous silica. V. The structure of vitreous silica: What have we learned from 60 years of diffraction studies? J. Non Cryst. Sol., 179: 84-115, doi: 10.1016/0022-3093(94)90687-4
Wright, A. C., & Thorpe, M. F. (2013). Eighty years of random networks. physica status solidi (b), 250: 931-936, doi: 10.1002/pssb.201248500
Huang, P. Y., Kurasch, S., Srivastava, A., Skakalova, V., Kotakoski, J., Krasheninnikov, A. V., Hoveden, R., Mao, Q., Meyer, J. C., Smet, J., Muller, D. A. & Kaiser, U. A. (2012). Direct imaging of a two-dimensional silica glass on graphene. Nano letters, 12: 1081-1086, doi: 10.1021/nl204423x
Huang, P. Y., Kurasch, S., Alden, J. S., Shekhawat, A., Alemi, A. A., McEuen, P. L., Sethna, J. P., Kaiser, U. A., & Muller, D. A. (2013). Imaging atomic rearrangements in two-dimensional silica glass: Watching silica’s dance. Science, 342: 224-227, doi: 10.1126/science.1242248
Kumar, A., Wilson, M., & Thorpe, M. F. (2012). Amorphous graphene: a realization of Zachariasen’s glass. Journal of Physics: Condensed Matter, 24: 485003, doi: 10.1088/0953-8984/24/48/485003
Sheng, H. W., Luo, W. K., Alamgir, F. M., Bai, J. M., & Ma, E. (2006). Atomic packing and short-to-medium-range order in metallic glasses. Nature, 439: 419-425, doi: 10.1038/nature04421
Gibson, J. M., Treacy, M. M. J., Sun, T. & Zaluzec, N. J. (2010) Substantial crystalline topology in amorphous silicon. Phys. Rev. Lett., 105: 125504, doi: 10.1103/PhysRevLett.105.125504
Turnbull, D. & Cohen, M. H. (1958) Concerning reconstructive transformation and formation of glass. J. of Chem. Phys., 29: 1049, doi: 10.1063/1.1744654
Meyer, J. C., Eder, F., Kurasch, S., Skakalova, V., Kotakoski, J., Park, H. J., Roth, S., Chuvilin, A., Eyhusen, S., Benner, G., Krasheninnikov, A. V., & Kaiser, U. A. (2012). Accurate measurement of electron beam induced displacement cross sections for single-layer graphene. Physical review letters, 108: 196102, doi: 10.1103/PhysRevLett.108.196102
Kotakoski, J., Meyer, J. C., Kurasch, S., Santos-Cottin, D., Kaiser, U., & Krasheninnikov, A. V. (2011). Stone-Wales-type transformations in carbon nanostructures driven by electron irradiation. Physical Review B, 83: 245420, doi: 10.1103/PhysRevB.83.245420
Crespi, V., Benedict, L., Cohen, M. & Louie, S. (1996) Prediction of a pure-carbon planar covalent metal. Phys. Rev. B, 53: R13303–R13305, doi: 10.1103/PhysRevB.53.R13303
Westenfelder, B., Meyer, J. C., Biskupek, J., Kurasch, S., Scholz, F., Krill III, C. E., & Kaiser, U. A. (2011). Transformations of carbon adsorbates on graphene substrates under extreme heat. Nano letters, 11: 5123-5127, doi: 10.1021/nl203224z
Turchanin, A., Weber, D., Buenfeld, M., Kisielowski, C., Fistul, M. V., Efetov, K. B., Weimann, T., Stosch, R., Mayer, J., & Golzhauser, A. (2011). Conversion of self-assembled monolayers into nanocrystalline graphene: structure and electric transport. ACS nano, 5: 3896-3904, doi: 10.1021/nn200297n
Huang, P. Y., Ruiz-Vargas, C. S., van der Zande, A. M., Whitney, W. S., Levendorf, M. P., Kevek, J. W., Garg, S., Alden, J. S., Hustedt, C. J., Zhu, Y., Park, J., & Muller, D. A. (2011). Grains and grain boundaries in single-layer graphene atomic patchwork quilts. Nature, 469: 389-392, doi: 10.1038/nature09718
Kim, K., Lee, Z., Regan, W., Kisielowski, C., Crommie, M. F., & Zettl, A. (2011). Grain boundary mapping in polycrystalline graphene. ACS nano, 5: 2142-2146, doi: 10.1021/nn1033423
Kurasch, S., Kotakoski, J., Lehtinen, O., Skákalová, V., Smet, J., Krill III, C. E., Krasheninnikov, A. V., & Kaiser, U. (2012). Atom-by-atom observation of grain boundary migration in graphene. Nano letters, 12: 3168-3173, doi: 10.1021/nl301141g
Robertson, A. W., Allen, C. S., Wu, Y. A., He, K., Olivier, J., Neethling, J., Warner, J. H., & Kirkland, A. I. (2012). Spatial control of defect creation in graphene at the nanoscale. Nature communications, 3: 1144, doi: 10.1038/ncomms2141
Torquato, S., & Stillinger, F. H. (2003). Local density fluctuations, hyperuniformity, and order metrics. Physical Review E, 68: 041113, doi: 10.1103/PhysRevE.68.041113
Lehtinen, O., Kurasch, S., Krasheninnikov, A. V. & Kaiser, U. (2013) Atomic scale study of the life cycle of a dislocation in graphene from birth to annihilation. Nature communications, 4: 2098, doi: 10.1038/ncomms3098